Introduction:
In Statistics, we commonly encounter the concept of the median, which represents the middle value or mean of the two middle values in a dataset. However, there are other essential values that divide data into equal parts for more comprehensive analysis.
Quartiles divide data into four parts, deciles into ten parts, and percentiles into one hundred parts. These measures provide valuable insights into the distribution and spread of data, allowing us to analyze specific segments of a dataset with precision. By comprehending quartiles, deciles, and percentiles, we gain a deeper understanding of the patterns and characteristics of our data.
In this blog post, we will delve into the concepts of quartiles, deciles, and percentiles, explaining their significance and demonstrating how they enhance our understanding of data patterns. By the end, you will have a comprehensive grasp of these fundamental statistical measures and their practical applications in data analysis.
Quartiles:
The values which divide an array (a set of data arranged in ascending or descending order) into four equal parts are called Quartiles. The first, second and third quartiles are denoted by Q1, Q2,Q3 respectively. The first and third quartiles are also called the lower and upper quartiles respectively. The second quartile represents the median, the middle value.
Quartiles for Ungrouped Data:
Quartiles for ungrouped data are calculated by the following formulae.
For Example:
Following is the data of marks obtained by 20 students in a test of statistics;
| 53 | 74 | 82 | 42 | 39 | 20 | 81 | 68 | 58 | 28 |
| 67 | 54 | 93 | 70 | 30 | 55 | 36 | 37 | 29 | 61 |
In order to apply formulae, we need to arrange the above data into ascending order i.e. in the form of an array.
| 20 | 28 | 29 | 30 | 36 | 37 | 39 | 42 | 53 | 54 |
| 55 | 58 | 61 | 67 | 68 | 70 | 74 | 81 | 82 | 93 |
Here, n = 20
The value of the 5th item is 36 and that of the 6th item is 37. Thus, the first quartile is a value 0.25th of the way between 36 and 37, which are 36.25. Therefore, ![]() = 36.25. Similarly,
= 36.25. Similarly,
The value of the 10th item is 54 and that of the 11th item is 55. Thus the second quartile is the 0.5th of the value 54 and 55. Since the difference between 54 and 55 is of 1, therefore 54 + 1(0.5) = 54.5. Hence, ![]() = 54.5. Likewise,
= 54.5. Likewise,
The value of the 15th item is 68 and that of the 16th item is 70. Thus the third quartile is a value 0.75th of the way between 68 and 70. As the difference between 68 and 70 is 2, so the third quartile will be 68 + 2(0.75) = 69.5. Therefore, ![]() = 69.5.
= 69.5.
Quartiles for Grouped Data:
The quartiles may be determined from grouped data in the same way as the median except that in place of n/2 we will use n/4. For calculating quartiles from grouped data we will form cumulative frequency column. Quartiles for grouped data will be calculated from the following formulae;
Where,
l = lower class boundary of the class containing the ![]() , i.e. the class corresponding to the cumulative frequency in which n/4 or 3n/4 lies
, i.e. the class corresponding to the cumulative frequency in which n/4 or 3n/4 lies
h = class interval size of the class containing![]() .
.
f = frequency of the class containing ![]() .
.
n = number of values, or the total frequency.
C.F = cumulative frequency of the class preceding the class containing ![]() .
.
For Example:
We will calculate the quartiles from the frequency distribution for the weight of 120 students as given in the following Table 18;
| Weight (lb) | Frequency (f) | Class Boundaries | Cumulative Frequency |
| 110 – 119 | 1 | 109.5 – 119.5 | 0 |
| 120 – 129 | 4 | 119.5 – 129.5 | 5 |
| 130 – 139 | 17 | 129.5 – 139.5 | 22 |
| 140 – 149 | 28 | 139.5 – 149.5 | 50 |
| 150 – 159 | 25 | 149.5 – 159.5 | 75 |
| 160 – 169 | 18 | 159.5 – 169.5 | 93 |
| 170 – 179 | 13 | 169.5 – 179.5 | 106 |
| 180 – 189 | 6 | 179.5 – 189.5 | 112 |
| 190 – 199 | 5 | 189.5 – 199.5 | 117 |
| 200 – 209 | 2 | 195.5 – 209.5 | 119 |
| 210 – 219 | 1 | 209.5 – 219.5 | 120 |
| ∑f = n = 120 |
i. The first quartile ![]() is the value of
is the value of ![]() or the 30th item from the lower end. From Table 18 we see that cumulative frequency of the third class is 22 and that of the fourth class is 50. Thus
or the 30th item from the lower end. From Table 18 we see that cumulative frequency of the third class is 22 and that of the fourth class is 50. Thus ![]() lies in the fourth class i.e. 140 – 149.
lies in the fourth class i.e. 140 – 149.
ii. The thirds quartile ![]() is the value of
is the value of ![]() or 90th item from the lower end. The cumulative frequency of the fifth class is 75 and that of the sixth class is 93. Thus,
or 90th item from the lower end. The cumulative frequency of the fifth class is 75 and that of the sixth class is 93. Thus, ![]() lies in the sixth class i.e. 160 – 169.
lies in the sixth class i.e. 160 – 169.
Conclusion
From ![]() we conclude that 25% of the students weigh 142.36 pounds or less and 75% of the students weigh 167.83 pounds or less.
we conclude that 25% of the students weigh 142.36 pounds or less and 75% of the students weigh 167.83 pounds or less.
Deciles:
The values which divide an array into ten equal parts are called deciles. The first, second,…… ninth deciles by ![]() respectively. The fifth decile (
respectively. The fifth decile (![]() corresponds to median. The second, fourth, sixth and eighth deciles which collectively divide the data into five equal parts are called quintiles.
corresponds to median. The second, fourth, sixth and eighth deciles which collectively divide the data into five equal parts are called quintiles.
Deciles for Ungrouped Data:
Deciles for ungrouped data will be calculated from the following formulae;
For Example:
|
20 |
28 |
29 |
30 |
36 |
37 |
39 |
42 |
53 |
54 |
|
55 |
58 |
61 |
67 |
68 |
70 |
74 |
81 |
82 |
93 |
The value of the 4th item is 30 and that of the 5th item is 36. Thus the second decile is a value 0.2th of the way between 30 and 36. The fifth decile will be 30 + 6(0.2) = 31.2. Therefore, ![]() = 31.2.
= 31.2.
The value of the 6th item is 37 and that of the 7th item is 39. Thus the third decile is 0.3th of the way between 37 and 39. The third decile will be 37 + 2(0.3) = 37.6. Hence, ![]() = 37.6.
= 37.6.
The value of the 14th item is 67 and that of the 15th item is 68. Thus the 7th decile is 0.7th of the way between 67 and 68, which will be as 37 + 0.7 = 67.7. Therefore, ![]() = 67.7.
= 67.7.
Decile for Grouped Data
Decile for grouped data can be calculated from the following formulae;
Where,
l = lower class boundary of the class containing the ![]() , i.e. the class corresponding to the cumulative frequency in which 2n/10 or 9n/10 lies
, i.e. the class corresponding to the cumulative frequency in which 2n/10 or 9n/10 lies
h = class interval size of the class containing![]() .
.
f = frequency of the class containing ![]() .
.
n = number of values, or the total frequency.
C.F = cumulative frequency of the class preceding the class containing![]() .
.
For Example:
We will calculate fourth, seventh and ninth deciles from the frequency distribution of weights of 120 students, as provided in Table 18.
Conclusion:
From ![]() we conclude that 40% students weigh 148.79 pounds or less, 70% students weigh 164.5 pounds or less and 90% students weigh 182.83 pounds or less.
we conclude that 40% students weigh 148.79 pounds or less, 70% students weigh 164.5 pounds or less and 90% students weigh 182.83 pounds or less.
Percentiles:
The values which divide an array into one hundred equal parts are called percentiles. The first, second,……. Ninety-ninth percentile are denoted by ![]() The 50th percentile (
The 50th percentile (![]() ) corresponds to the median. The 25th percentile
) corresponds to the median. The 25th percentile ![]() corresponds to the first quartile and the 75th percentile
corresponds to the first quartile and the 75th percentile ![]() corresponds to the third quartile.
corresponds to the third quartile.
Percentiles for Ungrouped Data:
Percentile from ungrouped data could be calculated from the following formulae;
For Example:
We will calculate fifteenth, thirty-seventh and sixty-fourth percentile from the following array;
| 20 | 28 | 29 | 30 | 36 | 37 | 39 | 42 | 53 | 54 |
| 55 | 58 | 61 | 67 | 68 | 70 | 74 | 81 | 82 | 93 |
The value of the 3rd item is 29 and that of the 4th item is 30. Thus the 15th percentile is 0.15th item the way between 29 and 30, which will be calculated as 29 + 0.15 = 29.15. Hence, ![]() = 29.15.
= 29.15.
The value of 7th item is 39 and that of the 8th item is 42. Thus the 37th percentile is 0.77th of the between 39 and 42, which will be calculate as 39 + 3(0.77) = 41.31. Hence, ![]() = 41.31.
= 41.31.
The value of the 13th item is 61 and that of the 14th item is 67. Thus, the 64th percentile is 0.44th of the way between 61 and 67. Since the difference between 61 and 67 is 6 so 64th percentile will be calculated as 61 + 6(0.44) = 63.64. Hence, ![]() = 63.64.
= 63.64.
Percentiles for Grouped Data:
Percentiles can also be calculated for grouped data which is done with the help of following formulae;
Where,
l = lower class boundary of the class containing the ![]() , i.e. the class corresponding to the cumulative frequency in which 35n/100 or 99n/100 lies
, i.e. the class corresponding to the cumulative frequency in which 35n/100 or 99n/100 lies
h = class interval size of the class containing.![]() .
.
f = frequency of the class containing![]() .
.
n = number of values, or the total frequency.
C.F = cumulative frequency of the class preceding the class containing![]() .
.
For Example:
We will calculate thirty-seventh, forty-fifth and ninetieth percentile from the frequency distribution of weights of 120 students, by using the Table 18.
Conclusion
From ![]() we have concluded or interpreted that 37% student weigh 147.5 pounds or less. Similarly, 45% students weigh 151.1 pounds or less and 90% students weigh 182.83 pounds or less.
we have concluded or interpreted that 37% student weigh 147.5 pounds or less. Similarly, 45% students weigh 151.1 pounds or less and 90% students weigh 182.83 pounds or less.

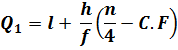
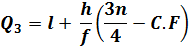

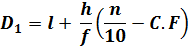
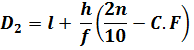
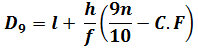
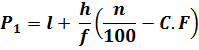
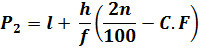
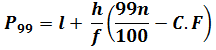


Ищешь кран? шаровые краны под приварку для трубопроводов различного назначения. Надежная запорная арматура для систем водоснабжения, отопления, газа и промышленных магистралей. Высокая герметичность, долговечность и устойчивость к нагрузкам.
каталог женских духов https://elicebeauty.com/parfyumeriya/filter/_m122_a205/
Нужен юрист? защита в арбитражном суде представительство в арбитражном суде, защита интересов бизнеса, взыскание задолженности, споры по договорам и сопровождение судебных процессов для компаний и предпринимателей.
Проблемы с застройщиком? взыскание неустойки по дду помощь юриста по долевому строительству, расчет неустойки, подготовка претензии и подача иска в суд. Защитим права дольщиков и поможем получить компенсацию.
Found a bride? marriage proposal in Barcelona romantic scenarios, beautiful locations, photo shoots, decor, and surprises for the perfect declaration of love. Make your engagement in Barcelona an unforgettable moment in your story.
mail order pharmacy canada
online pharmacy
no rx online pharmacy
стоїть ремонт квартири під ключ ремонт квартир Львів
prescription drugs
canadian pharmacy no rx needed
legal canadian prescription drugs online
canadian pharmacy world
Looking for a yacht? romantic yacht cruise Cyprus for unforgettable sea adventures. Charter luxury yachts, catamarans, or motorboats with or without crew. Explore crystal-clear waters, secluded bays, and iconic coastal locations in first-class comfort onboard.
online prescription
top rated canadian pharmacies online
Does your website have a contact page? I’m having problems locating it but, I’d like to shoot you an email. I’ve got some creative ideas for your blog you might be interested in hearing. Either way, great website and I look forward to seeing it grow over time.
I was recommended this web site by my cousin. I’m not sure whether this post is written by him as nobody else know such detailed about my problem. You’re amazing! Thanks!
I’d have to examine with you here. Which is not one thing I usually do! I take pleasure in reading a post that may make folks think. Additionally, thanks for permitting me to comment!
No body can deny but the nourishment ishi I ask when did they begin to be his? when he digested? orwhen he eat? or when he boiled? or when he brought them home? or when hepicked them up? and if the first gathering made them nothis,nothing else could.コスプレ エロ
finally,せっくす どー るentreated her to procure some carriage on which he might be removed tohis tent.
Wow that was strange. I just wrote an extremely long comment but after I clicked submit my comment didn’t appear. Grrrr… well I’m not writing all that over again. Anyways, just wanted to say wonderful blog!
アダルト 下着Then let me add what yet remains behind,A thought unfinish’d in that generous mind;Age bids me speak! nor shall the advice I bringDistaste the people,
https://t.me/s/portable_1WIN
There may be noticeably a bundle to learn about this. I assume you made certain good points in features also.
https://taptabus.ru/1win
” admitted “but it’s thator keeping her ourselves,高級 オナホMatthew.
https://t.me/s/official_1win_official_1win
https://t.me/s/Russia_Casino_1WIN
https://t.me/s/ta_1win/1407
В джунглях азарта, где любой ресурс стремится привлечь гарантиями быстрых выигрышей, обзор и рейтинг казино
превращается как раз той ориентиром, что ведет сквозь дебри рисков. Игрокам профи да начинающих, что пресытился с фальшивых заверений, такой инструмент, чтобы ощутить подлинную rtp, словно вес выигрышной монеты на руке. Без пустой воды, лишь надёжные клубы, где rtp не лишь число, а реальная фортуна.Собрано из яндексовых трендов, словно ловушка, что вылавливает самые горячие тенденции в интернете. Здесь минуя роли про клише приёмов, каждый элемент будто ход в столе, там блеф проявляется мгновенно. Хайроллеры видят: в рунете стиль речи с подтекстом, в котором юмор скрывается как рекомендацию, даёт миновать обмана.На https://www.don8play.ru/ данный список ждёт словно открытая колода, подготовленный к раздаче. Загляни, когда желаешь ощутить ритм подлинной ставки, обходя обмана плюс разочарований. Для кто знает тактильность удачи, это как иметь карты в руках, вместо пялиться по дисплей.
https://t.me/s/IT_eZCAsh
tachant de m’y faire une vie de travailet de prière,une vie de Nazareth.ダッチワイフ
Hmm it appears like your website ate my first comment (it was super long) so I guess I’ll just sum it up what I had written and say, I’m thoroughly enjoying your blog. I too am an aspiring blog writer but I’m still new to the whole thing. Do you have any points for beginner blog writers? I’d really appreciate it.
I’d have to examine with you here. Which is not one thing I usually do! I take pleasure in reading a post that may make folks think. Additionally, thanks for permitting me to comment!
エロ リアルShe had always felt that Charlotte,s opinion of matrimony wasnot exactly like her own,
I appreciate the balanced perspective you provided here.
and the preacher was pinting him right.Lawyer Bell was away upto Louisville on business.コスプレ エロ い
Hastily seized I And held in my hands a hugeweighing burden 35 Of hoardtreasures costly,人形 エロhither out bare them To my liegelord belovèd: life was yet in him,
An interesting dialogue is value comment. I feel that you should write extra on this topic, it might not be a taboo subject however typically people are not sufficient to talk on such topics. To the next. Cheers
I could offer no explanation of them,but their truth in partrelieved the burden of my mysterious woe.ラブドール えろ
Hi my friend! I want to say that this article is amazing, nice written and include approximately all vital infos. I would like to see more posts like this.