Introduction

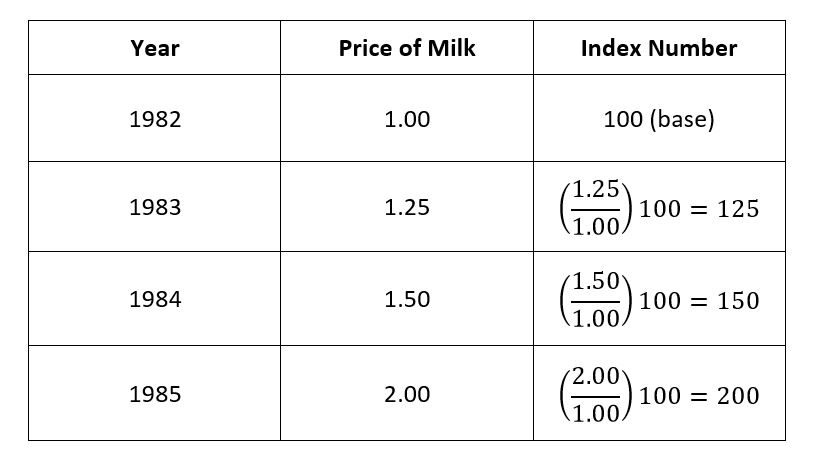
Often we want to know how certain variables like prices, production, etc. have changed over time and space. For example, we may like to compare the change in the average retail price of milk in 1985 with that in 1982 or we may like to compare the retail price of milk in Houston with that in Virginia or New Jersey. We may also like to know the increase in the yield of wheat in India during 1985 as compared to 1982.

We can easily compare such changes by expressing the price or quantity in a given period as percentage of the price or quantity in the base period, i.e. the period with which comparison is made. These percentages which compare changes in the prices of quantities at different periods of time with that of the base period, taken as 100, are very simple examples of what are known as Index Numbers as shown in the following table.

More difficult problems arise when we want to compare changes in a complex phenomenon like cost of living, total industrial production, wages etc. This involves comparing changes in the prices or quantities of many commodities. Since the prices or quantities of different commodities are in different units (e.g. wheat per mounds, cloth per yard, and many more) they cannot be compared directly. To measure changes in such situation, we combine the prices and quantities and find a single number. This single number which shows overall changes in a phenomenon is called an index umber or simple an index. Therefore, an index number is statistical measure which shows changes in a variable or a group of related variables with respect to time, geographical location or other characteristics such as income, profession, etc.

Simple and Composite Index Numbers

An index number that is computed foe a single variable is called a simple index number. For example, index numbers computed in above table are simple index numbers because they have been computed for a single commodity i.e. milk.  While on the other hand, an index number that is computed from two or more variables is called a composite index number. For example, wholesale price index numbers and consumer price index numbers are composite index numbers because they are computed for two or more variables (commodities).

Types of Index Numbers

Following types of index numbers are generally used

    1. Price Index Numbers

These index numbers shows changes in the wholesale or retail prices of a particular commodity or a number of commodities.

     2. Quantity Index Numbers

These index numbers measure changes in the volume or quantity of goods produced or goods exported or imported.

   3. Aggregate Index Numbers

These index numbers are used to measure changes in a phenomenon like cost living, industrial production etc. Such index numbers involve both quantities and prices of items appropriate to a given situation.

Uses of Index Numbers

An index number is device for measuring changes in a variable or a group of related variables. This device can be used whenever we want to compare changes in one or more variables in one period with those in others or in one region with those in others. For example, the index numbers of prices show changes in the wholesale or retail prices of commodities. These index numbers can therefore, be used to compare prices of one commodity with those in others at different periods of time or the prices in one part of the country with those in others during the same period of time.

The index number of industrial activity enables us to study the progress of industrialization in the country. The quantity index numbers show rise or fall in the volume of production, volume of exports and imports etc. the most well-known is the cost of living index or consumer price index. These cost of living index numbers are, in fact, the retail price indices. They show changes in the prices of goods generally consumed by people. They can therefore; help the government to formulate its price polices and take suitable economic measures to control prices. Moreover, these indices can be made a basis for regulation of wage rates and can be used by industrial and commercial organizations to grant dearness allowances and bonus to their employees in order to meet increased cost of living.

They are also used to evaluate the purchasing power of money. Index numbers are also being used for forecasting business and economic activities and in discovering seasonal fluctuations and business cycles. Although, index numbers are mainly used in the field of business and economics, they can also be applied in many other fields. For example, index numbers can be used in education sector to compare the intelligence of a student with that of an average student of his age or class. They can also be used to measure the effectiveness of teaching system.in the field of health, index numbers can be used to show the general health conditions of the people and to indicate the adequacy of hospital facilities.

Steps in the Construction of Index Numbers of Prices

Following steps are usually involves in the construction of index numbers of prices.

1. Definition of the purpose and scope.
2. Selection of commodities to be included
3. Collection of prices
4. Selection of the base period
5. Choice of average to be used
6. Selection of suitable weights

1. Definition of the Purpose and Scope

It is important to know that the purpose for which the index number is to be constructed is clearly known. The purpose should clearly state what changes are to be measured and why. A clear statement of purpose solves many problems. For example, if the purpose is to measure changes in the prices of foot-wear during 1986 in comparison to that of 1980, we should know what commodities to include, what prices to collect and from where to collect. The purpose may be general or special. A general purpose index can be put to more than one use while a special purpose index can serve only some special purpose. An index number designed to measure changes in the general price level in a country would be general purpose index number. On the other hand, an index number aimed at comparing the prices of particular items, e.g. cigarettes would be a special purpose index number. The object of the index number also determines its scope. A general purpose index number has a wide scope because it can serve more than one purposes. On the other hand, a special purpose index number has limited scope because it can be put only to some special use.

2. Selection of Commodity:

After having a determined object and scope of an index number, the next problem is the selection of commodities to be included. In a special purpose index number, the commodities to be included in comparing prices are usually few. There is, therefore, no question as to what commodities are to be selected. In a general purpose index number, the number of commodities which can be included in comparing the prices is very large. It is not practicable either from the point of view of cost or time to measure changes in the prices of all relevant commodities. A selected has, therefore, to be made. The commodities selected must possess following qualities;

1. Popular and important
2. Representative of the tastes and habits of the people
3. Unlikely to vary in quantity.

3. Collection of Prices:

This problem requires consideration of two points:

1. The prices to be used, and
2. The sources of price data

The term price in itself is a vague term because it may mean average “average price”, “wholesale price”, “retail price”, etc. It is, therefore, necessary to specify the prices to be used. In a general purpose index number, average wholesale prices are generally used.

As regards to the sources of price data, they are usually obtained from the markets where they are quoted. Prices should be obtained only from the representatives markets. Prices are sometimes also available from the price lists and trade journals. Before using such prices care must be taken to see that they are;

1. Reliable
2. Representative of the price prevailing in different markets
3. Comparable as regards the quality of the commodities in different markets and the units in which the prices are expressed

4. Selection of the Base Period:

As already explained in the beginning of this topic, the period with which prices in other periods are to be compared is called the base period or reference period. A base period is usually a year because a month or a quarter is too short as a period to be used a s base. There are two methods of selecting the base period;

1. Fixed base method
2. Chain base method.

Fixed Base Method:

In this method, the average price of a particular year or the average of the prices of a number of years is used as base. If a particular year price is used as a base, the base year should not be too far distant in the past. Further, the base year should be the normal year. By normal year we mean that a year which has economic stability and is free from crises caused by wars, floods, famines, strikes, etc. It is, however, true that no year is perfectly normal or ideal. For such reason, the average of the prices of a number of years should be used as a base.

To compute index numbers by fixed base method, the value of the base year is taken as 100. Index numbers for other years are computed by dividing the prices of a given year by the base year price. Values so obtained are called price relatives. Price relatives are expressed as percentages by multiplying them by 100. An average of the prices relatives of a year gives the index number of that year. Price relatives computed for a single commodity are called simple price relatives.

Chain Base Method

In the fixed based method, we compare changes in the prices of commodities in a number of years with that of the base year. As time passes, the tastes and habits of people change. The relative importance of the commodities also changes due to change in the quality of the commodities and discovery of some new commodities. For such reasons, it becomes necessary to shift the base year frequently. We may, therefore, use the chain base method in which price of the preceding year is taken as base. Price relatives computed by chain base method are called link relatives. Link relatives are also expressed as percentages.

The link relatives cannot be used directly used to make comparisons. To make comparisons of index numbers for a number of years, the link relatives are converted to fixed base. Index numbers so obtained are called chain indices. The chain index for a year is obtained by multiplying the average of the link relatives of that year by the chain index of the preceding year and then dividing the resulting product by 100. Obviously, the chain index for the base year is 100. However, if we are given the price relatives, then it is the average of the price relatives of the first year.

5. Choice of Average to be used:

When the price relatives or link relatives have been computed, they have to be average so as to get the index numbers. A choice of suitable average has, therefore, to be made. Any of the averages (arithmetic mean, median or geometric mean) can be used for index numbers. Arithmetic median or median may be used because they are easy to calculate and simple to understand. Further, the median is not affected by extreme values. Geometric mean is especially suitable for averaging price relatives because it gives equal weight to equal ratios of change and that the geometric mean of relatives in reversible.

6. Selection of Suitable Weights:

As we know that all the commodities which can be included in the construction of index numbers are not equally important. In order to give due regard to the importance of a commodity in the construction of index numbers, it is necessary to assign suitable weights to the commodities. Weights may be implicit or explicit. In implicit weighting, the price of the commodity whose importance is intended to be increased is quoted by a higher unit. For example, in case of building material, the price of cement may be quoted per 100 bags instead of per bag if the relative importance of the cement is to be increased and wages of labor may be quoted per week or per month instead of per day if the relative importance of labor is to be increased. Such an implicit weighing is, however, not realistic in a majority of the cases. Construction of the useful index numbers requires a conscious effort to assign to each commodity a weight in accordance with its importance in the total phenomenon that the index number is supposed to describe. The importance of the price of a commodity in the overall pictured described by an index number is generally determined by its quantity produced, consumed, bought or sold. We, therefore, use the quantities in the base year or given year or some other set of quantities as weights. Such a s weighting is called explicit weighting.

Common Notations