Definition
The median divides a frequency distribution into two halves. The median of set of values arranged either in ascending order or descending order of their magnitude is referred as the middle value. Median is denoted by ![]() ( X- childa).
( X- childa).
Explanation
Where the number of values in a data is odd, the median shall be the middle value. And where the number of values is even, the median shall be the mean of two middle values. Once the distribution is divided into two halve by way of median then the number of values greater than the median is equal to the values smaller than the median.
For Example
i. The median of values; 4, 5, 6, 8, 10, 11 and 12 is 8.
ii. The median of values; 4, 6, 7, 9, 11 and 13 is ![]()
From the above examples we have learned that when the number of values is odd, the median is the middle values and when the number of values is even, the median is the mean of the two middle values present in the data. In both the cases the median is the value of ![]() th item from either ends of the data which is being arranged in ascending or descending order.
th item from either ends of the data which is being arranged in ascending or descending order.
In example (i) n=7, and the ![]() th item or the 4th item from either sides is 8. And in example (ii), n=6 and the median which is
th item or the 4th item from either sides is 8. And in example (ii), n=6 and the median which is ![]() th or 3.5th i.e. half way between the 3rd and 4th from either end, is
th or 3.5th i.e. half way between the 3rd and 4th from either end, is ![]() .
.
In an array of values the position, the position of median could be determined by the following formula;
![]()
Median for Grouped Data
In case of frequency distribution the median is the value of ![]() th item from either end. Therefore, if we have 100 items in a frequency distribution, the median will be the value of the 50th item. In order to find the median from a frequency distribution, we need to form a separate column for cumulative frequency. The median will lie in the class which corresponds to the cumulative frequency in which
th item from either end. Therefore, if we have 100 items in a frequency distribution, the median will be the value of the 50th item. In order to find the median from a frequency distribution, we need to form a separate column for cumulative frequency. The median will lie in the class which corresponds to the cumulative frequency in which ![]() lies.
lies.
The formula for median in case of frequency distribution is as follows;
Where,
l = lower class boundary of the median class, which is corresponding to the cumulative frequency in which ![]() lies.
lies.
h = class interval size of the median class.
f = frequency of the median class.
n = number of values, or the total frequency.
C.F = cumulative frequency of the class preceding the median class.
For Example
The median for the following Table 14 will be;
Table 14
|
Classes |
Frequency (f) |
Class Boundaries |
Cumulative Frequency (C.F) |
|
0 – 9 |
2 |
-0.5 – 9.5 |
2 |
|
10 – 19 |
3 |
9.5 – 19.5 |
5 |
|
20 – 29 |
11 |
19.5 – 29.5 |
16 |
|
30 – 39 |
24 |
29.5 – 39.5 |
40 |
|
40 – 49 |
32 |
39.5 – 49.5 |
72 |
|
50 – 59 |
40 |
49.5 – 59.5 |
112 |
Here,
n =112
i = 10
f = 32
l = 39.5
So,
Another example for calculating median by the Table 15 is provided as follows;
Table 15
|
Class Marks (X) |
Frequency (f) |
Class Boundaries |
Cumulative Frequency (C.F) |
|
18.5 |
7 |
13.5 – 23.5 |
7 |
|
28.5 |
12 |
23.5 – 33.5 |
19 |
|
38.5 |
23 |
33.5 – 43.5 |
42 |
|
48.5 |
35 |
43.5 – 53.5 |
77 |
|
58.5 |
25 |
53.5 – 63.5 |
102 |
|
68.5 |
8 |
63.5 – 73.5 |
110 |
Here,
n =110
h = 10
f = 35
l = 43.5
So,

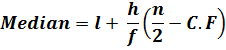


After exploring a handful of the blog articles on your site, I really appreciate
your way of writing a blog. I saved it to my bookmark website list and
will be checking back in the near future. Please check out my website too and
let me know what you think.
Great paintings! That is the type of info that should be shared across the internet. Disgrace on Google for now not positioning this post upper! Come on over and discuss with my web site . Thank you =)
Its such as you read my mind! You appear to know a lot approximately this, like you wrote the book in it or something. I feel that you simply could do with some to force the message home a little bit, however other than that, this is magnificent blog. A great read. I will definitely be back.
https://t.me/s/portable_1WIN
https://t.me/s/official_1win_official_1win
https://t.me/s/Russia_Casino_1Win
https://t.me/ta_1win/1268
https://t.me/s/iT_EZCaSh
В мире ставок, где каждый площадка норовит зацепить гарантиями быстрых джекпотов, рейтинг интернет казино россия
становится той самой путеводителем, что проводит через заросли обмана. Игрокам хайроллеров плюс дебютантов, что пресытился из-за фальшивых обещаний, это средство, чтобы ощутить реальную rtp, как тяжесть ценной ставки в руке. Без лишней воды, просто реальные клубы, там rtp не лишь число, а конкретная фортуна.Составлено на основе гугловых запросов, как ловушка, что вылавливает самые актуальные тенденции на сети. В нём нет роли для стандартных приёмов, любой пункт словно карта на столе, где обман выявляется мгновенно. Профи видят: на России тон речи на сарказмом, в котором юмор притворяется как рекомендацию, помогает миновать рисков.На https://don8play.artstation.com/projects/kNyzPA данный список лежит словно раскрытая колода, подготовленный для игре. Загляни, когда хочешь почувствовать ритм настоящей азарта, минуя иллюзий да разочарований. Игрокам что знает ощущение приза, такое будто держать ставку в руках, минуя пялиться в дисплей.
Hmm it appears like your website ate my first comment (it was extremely long) so I guess I’ll just sum it up what I wrote and say, I’m thoroughly enjoying your blog. I too am an aspiring blog writer but I’m still new to everything. Do you have any tips and hints for newbie blog writers? I’d definitely appreciate it.
I’ve been absent for some time, but now I remember why I used to love this website. Thank you, I will try and check back more often. How frequently you update your web site?