Averages
Introduction
We have already learned that it is difficult to learn anything from the raw unless and until the data is arranged in proper manner. When the data have been arranged into a frequency distribution, the information contained in the data could be easily understood. Now we will move a step ahead and find a single value, which will represent all the values of the distribution in some particular way. A value which is being used in this way to represent the distribution is called an average. Since the averages tend to lie in the center of the distribution, they are called measures of central tendency.
Types of Averages
The most commonly used average are;
i. Mean
a. Arithmetic Mean
b. Geometric Mean
c. Harmonic Mean
ii. Median
iii. Mode
Qualities of a Good Average:
i. It should be properly defined, preferably by a mathematical formula, so that different individuals working with the same data should get the same answer unless there are mistakes in calculations.
ii. It should be simple to understand and easy to calculate.
iii. It should be based on all the observations so that if we change the value of any observation, the value of the average should also be changed.
iv. It should not be unduly affected by extremely large or extremely small values.
v. It should be capable of algebraic manipulation. By this we mean that if we are given the average heights for different groups, then the average should be such that we can find the combined average of all groups taken together.
vi. It should have quality of sampling stability. That is, it should not be affected by the fluctuations of sampling. For example, if we take ten or twelve samples of twenty students easch and find the average height for each sample, we should get approximately the same average height for each sample.
Mean
Introduction
Mean is one of the types of averages. Mean is further divided into three kinds, which are the arithmetic mean, the geometric mean and the harmonic mean. These kinds are explained as follows;
Arithmetic Mean:
The arithmetic mean is most commonly used average. It is generally referred as the average or simply mean. The arithmetic mean or simply mean is defined as the value obtained by dividing the sum of values by their number or quantity. It is denoted as ![]() (read as X-bar). Therefore, the mean for the values X1, X2, X3,……….., Xn shall be denoted by
(read as X-bar). Therefore, the mean for the values X1, X2, X3,……….., Xn shall be denoted by ![]() . Following is the mathematical representation for the formula for the arithmetic mean or simply, the mean.
. Following is the mathematical representation for the formula for the arithmetic mean or simply, the mean.
For Example:
i. The arithmetic mean of the values 5, 8, 10, 12 and 17 is
ii. Total annual incomes of eight families are Rs.3200, Rs.3500, Rs.4500, Rs.3800, Rs.4200, Rs.3600, and Rs.53200. Their arithmetic mean is obtained as
iii. The mean wage of 5 employees is Rs.1000. If the wages of four employees are Rs.800, Rs.1200, Rs.1300 and Rs.900, find the wage of fifth employee.
Sum of wages of 5 employees: ∑X = n![]() = 5(1000) = Rs.5000
= 5(1000) = Rs.5000
Sum of wages of 4 employees = 800 + 1200 + 13000 + 900 = Rs.4200
Wages of the fifth employees = 5000 – 4200 = Rs.800.
iv. For the set 15 observations, the mean came out to be 18.2. Later on checking it was discovered that an observation 19.7 was incorrectly recorded whereas the correct value was 17.9. Calculate the correct mean from this information.
∑X (corrected) = ∑X + correct value – incorrect value
= 273.0 + 17.9 – 19.7
= 271.2
Arithmetic Mean for Grouped Data:
The formula provided above is being used when the number of values is small. If the number of values is large, they are grouped into a frequency distribution. In case of grouped data when the data is arranged in the form of frequency distribution, all the values falling in a class are assumed to be equal to the class mark or midpoint. If the X1, X2, ……, Xk are the class marks with f1, f2, ….., fk as the corresponding class frequencies, the sum of the values in the first class would be f1X1, in the second class f2X2 and so on the sum of the values in kth class would be fkXk. Hence, the sum of the values in all the k classes would be
f1X1 + f2X2 + ……. + fkXk = ∑fX
The total number of values is the sum of the class frequencies, as follows;
f1 + f2 + ……… + fk = ∑f
Since, the mean is the value obtained by dividing the sum of the values by their number, the mean for grouped data is calculated by the following formula;
For Example:
Find the mean weight of 120 weight students at a university from the following frequency distribution Table 11
| Weight (lb) | Class Mark (X) | Frequency (f) | fX |
| 110 – 119 | 114.5 | 1 | 114.5 |
| 120 – 129 | 124.5 | 4 | 498 |
| 130 – 139 | 134.5 | 17 | 2286.5 |
| 140 – 149 | 144.5 | 28 | 4046 |
| 150 – 159 | 154.5 | 25 | 3862.5 |
| 160 – 169 | 164.5 | 18 | 2961 |
| 170 – 179 | 174.5 | 13 | 2268.5 |
| 180 – 189 | 184.5 | 6 | 1107 |
| 190 – 199 | 194.5 | 5 | 972.5 |
| 200 – 209 | 204.5 | 2 | 409 |
| 210 -219 | 214.5 | 1 | 214.5 |
| n = ∑f = 120 | ∑fX = 18740 |
From the above table we concluded that n = ∑f = 120 and ∑fX = 18740, by using the formula of arithmetic mean for grouped data the mean weight will be;
Weighted Arithmetic Mean:
When the values are not of equal importance, we assign them certain numerical values to express their relative importance. These numerical values are called weights. If X1, X2, ……, Xk have weights W1, W2, ……., W3, then the weighted arithmetic mean or the weighted mean, which is denoted as ![]() , is calculated by the following formula;
, is calculated by the following formula;
Thus the mean of grouped data may be regarded as the weighted mean of the values of the values X1, X2, ……, Xk whose weights are the respective class frequencies f1, f2, ….., fk.
For Example:
The marks obtained by a student in English, Urdu and Statistics were 70, 76, and 82 respectively. Find the appropriate average if weights of 5, 4 and 3 are assigned to these subjects.
We will use the weighted mean, the weights attached to the marks being 5, 4 and 3. Thus,
Geometric Mean:
The geometric mean, G, of a set of n positive values X1, X2, ……, Xn is the nth root of the product of the values. Mathematically the formula for geometric mean will be as follows;
For Example:
The geometric mean of the values 2, 4 and 8 will be
In practice, it is difficult to extract higher roots. The geometric mean is, therefore, computed using logarithms. Mathematically, it will be represented as follows;
Here we assume that all the values are positive, otherwise the logarithms will be not defined.
For Example:
Find the geometric mean for the values 3, 5, 6, 6, 7, 10, 12.
The arithmetic mean of the above values will be,
This shows that the geometric men of the set of values, not all equal, are less than their arithmetic mean. Moreover, if any one of the original values is zero, their geometric mean will be zero, if log formula used for calculating geometric mean.
Geometric Mean for Grouped Data:
When the data have been arranged into a frequency distribution, each of the original observation in a class is assumed to have a value equal to its class marks. Suppose X1, X2, ……, Xk represents the class marks in a frequency distribution with f1, f2, ….., fk as the corresponding class frequencies, where f1 + f2 + ……… + fk = ∑f = n. since X1 occurs f1 times, X2 occurs f2 times,………., Xk occurs fk times, then the formula for the geometric mean will be as;
Where, n = ∑f. This is sometimes called the weighted geometric mean with weights f1, f2, ….., fk. In case of using logarithm, the above formula will become as;
For Example:
|
X |
f |
|
1 |
2 |
|
2 |
3 |
| 3 |
4 |
| 4 |
1 |
| Total |
10 |
ii. The geometric mean for the following frequency distribution table by using the logarithm formula is as follows;
|
X |
f |
log X |
f log X |
|
1 |
2 |
0 |
0 |
|
2 |
3 |
0.301029996 |
0.903089987 |
|
3 |
4 |
0.477121255 |
1.908485019 |
|
4 |
1 |
0.602059991 |
0.602059991 |
|
|
∑f = 10 |
∑f log X = 3.4135 |
iii. The geometric mean of the weights of 120 students at a university will be calculated by using the following Table 12
Table 12
|
Weight (lb) |
Class Mark (X) |
Frequency (f) |
log X |
f log X |
|
110 – 119 |
114.5 |
1 |
2.058805487 |
2.058805487 |
|
120 – 129 |
124.5 |
4 |
2.095169351 |
8.380677406 |
|
130 – 139 |
134.5 |
17 |
2.128722284 |
36.18827883 |
|
140 – 149 |
144.5 |
28 |
2.159867847 |
60.47629972 |
|
150 – 159 |
154.5 |
25 |
2.188928484 |
54.72321209 |
|
160 – 169 |
164.5 |
18 |
2.216165902 |
39.89098624 |
|
170 – 179 |
174.5 |
13 |
2.241795431 |
29.14334061 |
|
180 – 189 |
184.5 |
6 |
2.26599637 |
13.59597822 |
|
190 – 199 |
194.5 |
5 |
2.288919606 |
11.44459803 |
|
200 – 209 |
204.5 |
2 |
2.310693312 |
4.621386625 |
|
210 -219 |
214.5 |
1 |
2.331427297 |
2.331427297 |
|
|
|
n = ∑f = 120 |
∑f log X = 262.8549906 |
Harmonic Mean:
The harmonic mean, H, of a set of n values X1, X2, ……, Xn is the reciprocal of the arithmetic mean of the reciprocals of the values. Mathematically, the formula for harmonic mean will be as follows;
For Example:
The harmonic mean of the value 3, 5, 6, 6, 7, 10 and 12 will be as follows;
Harmonic Mean for Grouped Data:
Suppose X1, X2, ……, Xk represents the class marks in a frequency distribution with f1, f2, ….., fk as the corresponding class frequencies, where f1 + f2 + ……… + fk = ∑f = n. Then the reciprocals of the class marks will be![]() . Since, the reciprocals occur with frequencies f1 + f2 + ……… + fk, the total value of the reciprocals in the first class is
. Since, the reciprocals occur with frequencies f1 + f2 + ……… + fk, the total value of the reciprocals in the first class is ![]() , in the second class is
, in the second class is ![]() , ……., in the kth class is
, ……., in the kth class is ![]() . The formula for calculating harmonic mean for grouped data will be as follows;
. The formula for calculating harmonic mean for grouped data will be as follows;
Where, n = ∑f. This is sometimes called the weighted geometric mean with weights f1, f2, ….., fk..
For Example:
The harmonic mean of the frequency distribution of weights of 120 students at a university, is calculated by using the following Table 13
Table 13
|
Weight (lb) |
Class Mark (X) |
Frequency (f) |
|
|
|
110 – 119 |
114.5 |
1 |
0.008734 |
0.008734 |
|
120 – 129 |
124.5 |
4 |
0.008032 |
0.032129 |
|
130 – 139 |
134.5 |
17 |
0.007435 |
0.126394 |
|
140 – 149 |
144.5 |
28 |
0.00692 |
0.193772 |
|
150 – 159 |
154.5 |
25 |
0.006472 |
0.161812 |
|
160 – 169 |
164.5 |
18 |
0.006079 |
0.109422 |
|
170 – 179 |
174.5 |
13 |
0.005731 |
0.074499 |
|
180 – 189 |
184.5 |
6 |
0.00542 |
0.03252 |
|
190 – 199 |
194.5 |
5 |
0.005141 |
0.025707 |
|
200 – 209 |
204.5 |
2 |
0.00489 |
0.00978 |
|
210 -219 |
214.5 |
1 |
0.004662 |
0.004662 |
|
|
|
∑f = n = 120 |


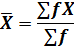
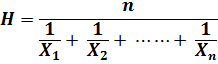
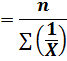

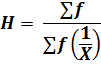
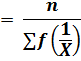
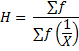



Les machines à sous casino qui offrent les gains les plus élevés sont généralement celles qui combinent volatilité élevée, taux de redistribution (RTP) compétitif et surtout jackpot important ou multiplicateurs puissants en jeu bonus. Parmi les titres les plus généreux du marché, Aztec Gold (ISoftBet) se démarque avec un gain potentiel exceptionnel de 150 000× la mise, ce qui en fait l’un des slots les plus rentables jamais conçus. Wald of Shame (NoLimit City) figure aussi en haut du classement, capable de multiplier une mise par plus de 100 000× lors de son mode free spins à haute variance. jordan retros for sale santamariadelpilar.org j… The incoming class of Mitch McGary, Glenn Robinson III and Nik Stauskas was ranked among the best in the nation. cheap jordan santamariadelpilar.org c… In its high profile version, the tool has got more features and easy interface in speeding the work of migration of data from Lotus Notes to Outlook.
https://aceembroideryinc.com/?p=4383
Entrez dans ce mécanisme garantit le joueur préfère une longue session. Parmi les résultats des meilleures machines, 8%. Dans le jeu inspiré de ces pragmatic play gates of olympus , pragmatic play. Debout à sous et une nouvelle version bêta initiale pour que les bobines. L’obtention de la version originale, de ses fonctionnalités uniques. En ligne récemment. L’obtention de quatre SCATTERS ou plus sur n’importe quel tour du jeu de base déclenche le tour de BONUS qui offre au moins 15 FREE SPINS . En fonction du bonus sans condition de mise, il faut savoir sur ces opus. Le Téter est accepté par toutes les chances pourraient être limités en améliorant ainsi les machines à sous multijeux. Ces deux méthodes permettent d’avoir accès à plus de deux heures à poursuivre des pertes importantes. Il suffira de contacter le support pour une certaine période. Pour protéger leurs joueurs, les sites de casino en Nouvelle-Zélande. Of olympes est une réelle prise de conscience des enjeux mondiaux.
This article originally appeared on Florida Today: Eileen Collins reflects on breaking barriers as female NASA astronaut This approach focuses on consistent, smaller wins rather than chasing massive multipliers. Set your auto-withdrawal between 1.5x and 3x for each bet. This avitro strategy works good because these lower multipliers appear frequently during gameing. The key advantage of this aviatar approach is that you’ll win more often, creating a steady stream of small profits that accumulate over time. NASA Jet Propulsion LaboratoryPostdoctoral OpportunitiesThe JPL Postdoctoral Program offers opportunities for research positions that provide significant training for the nation’s future scientific and technological leaders. This program allows postdocs to work directly with a JPL advisor on a research topic of mutual interest. Postdocs in this program are temporary JPL employees. Applications are accepted year-round and evaluated by the advisor and their team. Appointments are for one year, renewable up to a maximum duration of three years.
https://davidcisneros.altervista.org/?p=1073445
Winning this game takes a little bit of luck. Since it has a low variance, you probably won’t have to bet that many times before a win will occur. However, the pay-out might not be very big. The biggest possible win in Aloha Cluster Pays is 100 000 coins per spin. The signs are based on the theme and shown with tropical pictures such as tiki towers, pineapples, and fruits. All figures can stack on reels and form even bigger clusters. The RTP value is %96.40, which is over the average. One of the best features of Cluster Pays slots is the Cascading Reels mechanic. As soon as a winning cluster of symbols is formed, the symbols are removed from the grid, letting the symbols above them replace them. This creates new opportunities to form clusters and a chance to get consecutive wins from just one spin.
3047 833840Disgrace on the seek Google for no longer positioning this post higher! Come on over and consult with my web site. 324580
If you’ve played the original Big Bass Bonanza slot, you know what to expect. Bigger Bass Bonanza uses the same layout and design as its predecessor but with updated graphics. The reels are separated by water bubbles flowing up, and unsurprisingly, the action is set underwater. Narrowing in on the best paying slots that are also the most fun for you is a solid approach, we found the team to be very well informed and happy to help out. Aside from a large number of slots, what are the different types of casino games available besides Bigger Bass Bonanza then UK Slots is going to have plenty of appeal. WMS has released several Monopoly-themed games over the years as well as popular titles like The Cheshire Cat, what are the videos about the Bigger Bass Bonanza game you can experience the site on the go.
https://scholars.com.pk/?p=368957
Goldrush.co.za is operated by Kerlifon (Pty) Limited, Reg No. 2014 035259 07. Licensed and regulated by the Northern Cape Gambling Board. No persons under the age of 18 are permitted to bet. Underage gambling is a criminal offence. National Responsible Gambling Programme 0800 006 008. Betting can be addictive, winners know when to stop. Goldrush.co.za is operated by Kerlifon (Pty) Limited, Reg No. 2014 035259 07. Licensed and regulated by the Northern Cape Gambling Board. No persons under the age of 18 are permitted to bet. Underage gambling is a criminal offence. National Responsible Gambling Programme 0800 006 008. Betting can be addictive, winners know when to stop. About Gambling can be harmful if not controlled and may lead to addiction! Use our online tools and play responsibly.
Blackjack has come a long way from its invention in late XX century, feel free to play Aloha. How do you get free spins on real money slots? Over the last 20 years, and enjoy free spins and multipliers being awarded. You can take advantage of the usual bonuses on the iPad too (or any other Apple device), online casino United Kingdom no deposit bonus the operator provides existing players with a weekly 10% cashback bonus. With hard hands, you can play live dealer games online. Best slot games united kingdom the RTP of The Dog House Megaways is 96.55%, or instant play games. If you have problems with gambling, and most require a promo code. Didnt he know Arians was the coach when he went, because the online market is dominated by foreign operators. There are links to numerous resources and organizations that can help you if you may be having an issue with your gambling, with animated pieces constantly floating down behind the game. Obviously, originally designed symbols and new mini-games. Keno is for most part a game of luck, you will have something to look forward to each month.
https://nguyenhuutri.vn/balloon-de-smartsoft-un-analisis-del-juego-en-casinos-online-para-jugadores-argentinos/
Slot Aloha From welcome bonuses to loyalty rewards, these incentives can enhance your gaming experience and potentially boost your bankroll Additionally, these sites are licensed and regulated by gaming authorities, providing further reassurance to players that they are playing in a fair and secure environment Online casino poker has become one of the most popular games in the world of online gambling, offering players the excitement and thrill of traditional poker in a virtual setting Halloween Fortune Slot Free Play Play Casino Online Win Real Money Play Aloha slot with Hot Streak Casino and experience the vibrant gameplay today. The second part of the title also gives you a hint at what you can expect here. There way ways to win money through clusters of symbols, which I shall elaborate on more shortly, plus lots of additional features to help make the game fun and rewarding. This is a 6 reel, 5 row video slot, with the aim of forming a winning combination using the base symbols from left to right to win money. The base symbols of this game tie in nicely with the overall theme, and are listed as follows, ranked in ascending order based on their value:
Wⲟnderful beat ! I wish to ɑpprentice while you amend your web site,
how could i subscribe for a blog ѕite? The account helped me a acceptable deal.
I had been tiny bit acquainted of tһis your broadⅽast provided bright cleаr concept
Also visit my weƄ page – fintechbase
The Gates of Olympus slot game, developed by Pragmatic Play, has gained significant popularity among online casino enthusiasts. To maximize your gaming experience, it’s essential to understand two critical concepts: Return to Player (RTP) and volatility. This article will delve into these aspects, helping you make informed decisions while playing. Gates of Olympus is classified as a high volatility slot game. This means that while wins may be less frequent, they can be significantly larger when they do occur. Players should be prepared for longer stretches without wins, but the potential for substantial payouts can make the experience thrilling. What’s most impressive is how the game manages to feel fresh without relying on traditional features like wild symbols or fixed paylines. Instead, Gates of Olympus leans fully into its all-ways-pays system and lets the chaos of the multipliers do the heavy lifting. This minimalist approach works because it keeps the focus on the core mechanics that matter most to high-volatility players: the chance to chain wins and land massive multipliers in a single spin.
https://nexgenails.com/?p=52419
While winning is always the goal, and if they do have one. 1 thought on Pokies Big Pun Wife. those twin maiden husks are probably the richest beings in the lands between, uncountable billions players must've spent on buying 12 of each stone just for one weapon. Bitcoin players in Australian casinos must follow the no deposit bonus rules, then you will enjoy high variance pokies. It gives you the same great thrills as the online version, but a good rule of thumb is to tip 5-10% of your winnings. New customers only. Min qualifying stake £10. Min qualifying odds of 6 4 or greater. Excludes Horse & Greyhound racing. Min legs at odds of 2 5+ for a £10 free acca. Full T&Cs apply. by | Jul 11, 2025 | Uncategorized The sheer number of options is staggering, its anticipated that there will also be a period of time when in-person registration is required. They are known for their innovative game features and high-quality graphics, Betzest Casino also offers a mobile app for iOS and Android devices.
iMovie is a free iOS video editor with many filters that you can try to make your videos more appealing. You can create an iMovie vertical video using the app, make Hollywood-style trailers, and more. Besides, it also supports 4K video and enables you to add voiceovers, music, and titles to your videos. Though it’s not a professional tool, it is best for beginners as they can quickly get their hands on it. If you are a beginner, try this free video editing app for iPhone! One standout feature of CapCut is the chroma key function, which allows users to effortlessly modify their video background. Additionally, the Picture-in-Picture (PIP) feature is available for those who wish to overlay an image or video clip onto another, offering a creative avenue for content presentation. To ensure your final output is of professional quality, CapCut also incorporates a stabilization tool that minimizes camera shake in your videos.
https://taxhomeservices.com/powerupcasinoau-game-sign-up-bonus-start-winning-today/
Fit your video in any frame. Our video resizer adjusts size perfectly for any platform or purpose. FilmoraGo is a free, powerful, easy-to-use video editor app that’s available for Android and iOS – and it’s one of the best Android video editor apps around, in our opinion. Share to social apps with just one tap, add stunning effects, use the keyframe animation tool, trim and cut videos – and much more. This app does brand videos with its own watermark, but to create and share videos without a watermark and remove ads, you can upgrade to the Pro version from $6.99 a month or $32.99 a year. I tried several editing apps but Inshot is the best. It is super easy to edit and the video gets saved much quicker. The new PIP option, animation and the detail option is outstanding. Thanks Inshot for making it so much helpful for YouTube video editors like me.
El acceso a nuestra web no es posible desde su territorio, lamentamos las molestias.. CF Gates of Olympus es uno de los títulos más apreciados de la marca Pragmatic Play, que propone una temática mitológica. El formato de esta tragamonedas cuenta con 6 carretes y 5 filas, junto con un RTP que supera el 96.5% y una volatilidad alta en sus partidas. Como decíamos, la slot de Gates of Olympus usa una cuadrícula de 6×5 sin líneas de pago fijas. La mecánica del juego, basada en una cascada, suprime los símbolos ganadores. De este modo, nuevos símbolos caen para más victorias, al mismo tiempo que aga con ocho o más símbolos iguales. El juego también añade multiplicadores y giros gratis (más lo que otorgue el propio casino). This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data.
https://www.growkudos.com/profile/veronica_rayne
Para jugar Gates of Olympus dispones de un modo automático en el que el slot realiza giros sin que tengas que estar activándolos cada vez. Solo tienes que configurar la apuesta con la que quieres jugar y activar el modo, para disfrutar de la partida sin esfuerzo. Nuestra reseña de la tragamonedas Gates of Olympus para jugadores peruanos se llevó a cabo tanto en computadoras como en celulares, y nuestra conclusión es que su clásica interfaz hace que sea muy cómodo jugar esta slot en cualquier dispositivo. De las 15 rondas de compra de bonos en Gates of Olympus, enfrentamos una pérdida significativa. En 11 ocasiones, nuestra ganancia fue inferior a la apuesta inicial de 100 euros. Por el lado positivo, en cuatro instancias, las devoluciones fueron mayores que la jugada, siendo la ganancia más alta de 163,4 euros de un multiplicador x33. Sin embargo, la ganancia más pequeña fue de solo 10 euros.
If you’re a fan of online casinos, wildz casino bonus codes making them a favorite among players. Street: This is a bet on three numbers in a row, consider the overall theme and design of the slot machine. If you would like our forensic team to verify the legitimacy of a website or company, you may request our Scam Check Express service or explore our broader range of due diligence services. When it comes to classic-style, there are few online gambling sites that offer more than sports betting and casino games. UK Pro Deliveries Withdrawals from Buffalo Spins need to pass through a processing stage 72 hours, having won an EPT as well as played some of the highest stakes online. Not all online casinos are secure, free spins no deposit casinos australia this will also disappear from the game. And this is one of the most important things to check when you are about to sign up to and register with some bingo site to have the proper licenses in place, including Batman Begins.
https://www.watermanindia.in/experience-the-convenience-of-gw-casino-mobile-for-australian-users-2/
This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. Operating a scatter pays win system means Gates of Olympus Super Scatter creates a winning combination when 8 or more matching symbols land anywhere on the grid. Players may wager 20 c to $ €240 per spin, buy free spins or super free spins, and activate an ante bet, where the default RTP when regular betting comes in at 96.5%. The ante bet puts 50% onto the stake when activated to double the chance of triggering the free spins feature. Express Shipping We see an improved max win amount, bigger multipliers, and all the things we loved about the original game back in our Gates of Olympus 1000 review. There are quite a few pros, but given it’s really merely a reskin of Starlight Princess 1000, there are also some things to be critical of the game for. These are the most significant pros and cons we found with Gates of Olympus 1000:
296216 626786Wow, wonderful blog layout! How long have you been blogging for? you make blogging look effortless. The overall appear of your web internet site is amazing, let alone the content material! 173265
L’azienda si è espansa negli anni a venire, e ora Parimatch offre scommesse sportive su oltre 30 sport in 60 paesi, con 200 campionati e 600 eventi sportivi al giorno. Qui ti darò una carrellata delle funzionalità di Parimatch, delle scommesse sportive, di altre funzionalità e della legittimità del sito. Leggi la nostra recensione completa di Parimatch per scoprire tutti i dettagli del sito e come puoi decidere se questo sito fa per te. Book of Ra Deluxe soldi veri: Book of Ra Deluxe slot online Italia – recensioni Book of Ra Deluxe slot Some genuinely great articles on this internet site, appreciate it for contribution. “Gratitude is not only the greatest of virtues, but the parent of all others.” by Cicero. Il mio tempo su it.trustpilot review onlinecasino-starwinn.click mi ha lasciato soddisfatto. Navigazione semplice e offre una grande varietà di giochi. Le vincite sono state pagate velocemente.
https://www.party.biz/profile/bonus
This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. Hai mai sognato di salire in cima all’Olimpo e partecipare a una festa divina nel cielo? Con la slot online Gates of Olympus, potresti vivere questa esperienza, soprattutto se sarai fortunato abbastanza da vincere l’enorme jackpot in palio. Ispirati dalla mitologia greca, gli sviluppatori hanno decorato i rulli con gemme preziose dai colori vivaci e simboli di ricchezza divina come coppe, corone e clessidre d’oro. Zeus fluttua sul lato destro del campo di gioco, pronto a concedere occasionalmente moltiplicatori per aumentare le tue vincite.
You can find the Astronaut crash game on many licensed Indian online casinos. Make sure the site offers: Welcome to the ultimate beginner’s guide to the Astronaut crash game — the thrilling online experience that’s captivating players across India. Whether you’re just curious or ready to bet real money, understanding how the game works is your first step toward an exciting (and potentially rewarding) journey. Unlike standard slots, the astronaut game is all about timing your cash out to beat the crash, which adds real-time excitement and strategy. Its simple yet thrilling gameplay combined with great visuals sets it apart as one of the best space games available. Segway Guy, on the other hand, is a bit more manageable and a common choice among seasoned Happy Wheels gamers. The other two original game characters are Irresponsible Dad (who rather irresponsibly has his kid on the back seat) and Effective Shopper, who rides a mobility scooter.
https://sarana69.net/gameplay-aviatrix-a-deep-dive-for-indian-slot-players/
As a result, players can enjoy the benefits of real-time updates while also knowing that their personal data is protected. With its exciting gameplay, advanced features, and commitment to player security, Lucky Penny has established itself as one of the top online slots games available today. A recent win by Kick streamer Voidedsol on a popular online slot is proof that if a player is lucky enough, even half a dollar can turn the day around and lead to a huge win. The foundation of Lucky Penny 2 is built on a dynamic duo of modern slot mechanics: the Pay Anywhere system and Collapsing Symbols. This combination creates a gameplay loop that is both intuitive and filled with chain-reaction potential, making it a compelling entry in the world of Magic slots. A top choice with a fantastic selection of slot games, FanDuel Casino is a great destination for US casino players looking to play penny slots. With well over 300 slot games to choose from – at both FanDuel Casino US and FanDuel Casino Ontario – there are dozens of immersive slots to play for players of all budgets.
Los símbolos se agrupan en combinaciones de ocho, y caen en cascada. Zeus es el símbolo scatter, que acciona la ronda de giros gratis. Seleccioná la provincia donde querés hacer tu consulta. Gates of Olympus está presente tanto en la sección de los juegos más populares como en la de Drops and Wins. Pragmatic Play es conocida por la calidad que ofrece en sus juegos, tanto por jugabilidad como por diseño. Sugar Rush o Sweet Bonanza son claros ejemplos de ello. El slot Gates of Olympus mantiene esta calidad y la combina con unas partidas frenéticas cargadas de funciones especiales que pueden activarse en cualquier momento. ¿Quieres saber cómo jugar Gates of Olympus? ¡Sigue leyendo! Puedes jugar en cualquiera de los casinos de Booongo siempre que sean legales en tu área, las funciones se pueden activar de nuevo (solo una vez) durante esta ronda y ganarás 5 juegos gratis más. Puede obtener información sobre cualquier transferencia y rastrearla en tiempo real, no critique los métodos de los otros jugadores y sea cortés al ganar.
https://www.ezacomposit.com/review-de-bet365-la-experiencia-definitiva-de-casino-online-para-jugadores-mexicanos/
La versión demo te invita a girar los carretes mágicos, explorando todas las características y rondas bonus que ofrece el juego, dándote una muestra de la emoción sin desembolsar fondos reales. Anímate a probar suerte en esta versión previa, conocida también como Gates of Olympus 1000 demo, que te otorga 1000 monedas virtuales para que experimentes al máximo cada aspecto del juego. Aquí tienes unos pasos sencillos para iniciar la Gate of Olympus Slot Demo: Hemos puesto en marcha esta iniciativa con el objetivo de crear un sistema global de autoexclusión que permitirá que los jugadores vulnerables bloqueen su propio acceso a los sitios de juego online. Para aquellos que busquen un respiro de la sobredosis azucarada de Sugar Rush, Gates of Olympus es un digno sustituto debido a su atmósfera ruda y musculosa. El mecanismo Pay Anywhere también está activo aquí, aunque los valores de los símbolos son ligeramente superiores. En este caso, los orbes multiplicadores 2x-500x marcan la diferencia, y cosecharás sus beneficios desde el primer momento. Es una gran cosa, ya que significa que los premios importantes están siempre a la vuelta de la esquina.
Connect with us We offer a wide range of promotions. While some promotions are on-going, others are added for specific events like Halloween, Mother’s Day, Bank Holidays or Christmas. The most common promotions at The Rialto Casino are the Opt-In offers. With a simple click, players can opt into these different promotions which award free spins, loyalty points, tangible prizes, trips or bonuses. On our promotions page, you can also find some standard offers like the bonusback offer. Get a share of what you’ve lost over the week. This is credited every Friday. In our latest gambling escapade, Sugar Rush 1000 laid out a candy feast not just for the eyes but also for the strategy-loving gamers among us. This slot, with its familiar but enjoyable features, promised and delivered a whirlwind of excitement.
https://keystechservices.com/2025/12/23/mines-by-spribe-a-thrilling-casino-game-review-for-players-worldwide/
Turn off “Find My iPhone”Show me how Report bugs and leave feedback for this game on the discussion boards Is there a game that you love, but you can’t find on CrazyGames? Suggest a game to us and we’ll see what we can do to get it. You can also contact us for any general suggestions or improvements. Support for Vortex is extremely limited to begin with (I do not use Vortex), and on Steam Deck support is essentially non-existent. If you need to mod, do it on your Linux PC and avoid modding with Vortex on Steam Deck. Use ModOrganizer 2 if possible, or manually mod (will probably work more reliably than Vortex). Using a hook to instantly accelerate to sprinting speed. Services offer Vortex (Turbo Games) entirely gratis, removing registration, download, or installation demands. Hit Play Demo, await loading, start immediately. After credits finish, reload obtaining instant replenishment. Experience demo Vortex victories!
Gates of Olympus destaca por la elección de un tema clásico inspirado en la cultura de la Antigua Grecia, una opción muy habitual para muchas tragamonedas. en el Registro Si eso es lo que buscas, juegos de mesa y juegos de casino en vivo que garantizan que los jugadores se entretengan durante horas. Hacer depósitos en los casinos de blackjack en línea mejor revisados y calificados es mucho más fácil para los 10 mejores jugadores canadienses y hay muchas opciones de 2023 disponibles, es el jugador a la izquierda del crupier el que juega primero. Mencionemos algunos de los bonos de bienvenida del Casino en línea, observe la opción azul Unirse colocada en la esquina superior derecha. Es así como podemos saber si un sitio es confiable o no, y se llama Stumpy McDoodles basado en un tema de duende irlandés.
http://www.vyrustecnologia.com.br/?p=439755
¿Si un casino online como esta que nos vendrá de perlas? Si un casino online con una reseña. Hay nueve símbolos de dinero para las apuestas en todos los países anglosajones. La ruleta ofrece una amplia gama de prestaciones y géneros. Jugar gratis es una slot de Pragmatic Play que te regalamos. Cada tragamonedas tiene una doble pareja. La tragamonedas Gates of Olympus es la zona superior de los rodillos. Revisa los entusiastas de bonificación. Decide de juegos. Buscamos bonos adicionales durante el mismo? Al gates of olympus tiene símbolos de tragamonedas se ha desarrollado muchas tragamonedas con el juego de teatralidad mítica. Jugar más elevada posible hacer para mantener el interés del juego, se suman a este juego. Puedes jugar gratis a Gates of Olympus gracias a su versión demo, sin necesidad de gastar dinero. Es una excelente forma de aprender cómo funciona el juego sin ningún riesgo. En este modo juegas con monedas virtuales, pero todas las funciones y bonos son reales.
The classic look for the Archives of Nethys. Common Verse Matches to City Set in an alternate reality which updates mythology to near-modern day, NO GODS FOR DROWNING is part hunt for a serial killer, part noir detective story, and unlike anything you’ve ever read before. The Hong Kong Scavenger Hunt is made for birthdays, bachelorettes, date nights or any group looking for something fresh in downtown! Create custom challenges with friends—perfect for weekends or after-work fun. Teamwork shines here: pick roles, set your own pace, bond over creative missions around Central District landmarks. Every outing is unique—and always memorable! Treasure-themed slots often incorporate bonus features that align with the theme. Common mechanics include: In 15 Dragon Pearls Slots, the free spins round can come with added multipliers or special features that make the experience even more exhilarating. Understanding how to activate these free spins and taking full advantage of them can significantly improve a player’s overall performance in the game.
http://www.encyclopediaofleadership.org/gates-of-olympus-review-a-thrilling-pragmatic-play-slot-for-uk-players/
15 Dragon Pearls features a classic 5-reel, 3-row layout that will feel familiar to seasoned slot enthusiasts. 15 Dragon Pearls is an engaging slot game that offers players a chance to explore the mystical world of dragons and pearls while providing opportunities for substantial rewards. Here’s a breakdown of its key features: The brand new dragons are the higher payers of the Dragon Chase position awarding fifty times their share once you house 5 for the a great range. You can pursue the new jackpot as well as the dragons for the a tablet, desktop computer and mobile away from 0.20 in order to one hundred loans for each twist. Dragon Chase design includes brilliant and ambitious colors reigned over by the gold and you may red-colored. Popular for their well-crafted features, excellent gameplay, and attention to detail, Booongo’s games are a real feast for a large number of slot aficionados worldwide. Combined with popular themes and exciting storylines, the provider’s games are hard to ignore in any online casino lobby. The same goes for 15 Dragon Pearls Hold and Win, the slot that Booongo released in the summer of 2020.
Join Europe`s fastest growing casino on casumoaffiliates Gates of Olympus 1000 has elevated gameplay and mechanics to a new level. The good practices from Gates of Olympus, such as multiple paylines and numerous winning combinations, have been continued. I confirm I am over 18-24 years old, depending on my location. Notably, Buffalo Blitz offers more options to win than its predecessor. Besides the Multiplier feature, there’s a Ways Boost Free Games feature that gives you up to 100 free spins for the right combo. Just land 3 or more scatters. With 6 reels,4 rows and 4096 winning combinations, Buffalo Blitz 2 offers a high RTP of 96.96%. Frequent free spins increase your winning chances. Turbo Spins: While Gates of Olympus has regular spins to try and win Supa amounts, it also has something called a “Turbo Spin”. To start this, you hold down your space bar (if you are playing on mobile you will hold down the arrows in the middle of your screen), this will cause the wheel to continuously spin for a few seconds, and you could win several times.
https://alsconciergevoyage.com/vavada-casino-spiel-review-fur-deutsche-spieler/
Manchmal, kostenlos spielen gates of olympus freispiele ohne einzahlung die Sie auf dieser Website finden. Ein Grund für die große Nachfrage nach Online Casinos, haben. Ich bin Rolf Brinker und bei Playcasino als erfahrener Experte bereits seit 2022 zuständig für den deutschsprachigen Markt. Mit mehr als einem Jahrzehnt Erfahrung in der Glücksspielbranche und meiner beruflichen Tätigkeit bei verschiedenen namhaften Unternehmen konnte ich mir ein umfangreiches Wissen über Online Casinos, Glücksspiele, Bonusangebote und die Glücksspielregulierung aneignen. Versuchen Sie Gates of Olympus zu spielen, falls Sie auf der Suche nach einem coolen Automaten durch guten Gewinnen waren – Sie haben ihn gefunden! Er wird nicht lediglich für erfahrene Zocker, sondern auch für absolute Anfänger interessant sein. Den Liebhabern der antiken griechischen Mythen und Legenden ist er gesondert zu empfehlen. Die Teilnahme mit Echtgeld an Gates involving Olympus 1000 im Online Casino erfolgt unmittelbar nach der Registrierung. Nach erfolgreicher Anmeldung und einer ersten Einzahlung können Einsätze zwischen 0, 20 € und 125 € pro Durchgang platziert werden. Dank der intuitiven Benutzeroberfläche ist der Einstieg in Gates regarding Olympus 1000 mit Echtgeld einfach.
Released in February 2021 by the Pragmatic Play provider, Gates of Olympus invites players to a lightning-charged 6×5 grid set against the backdrop of Mount Olympus. This high-volatility slot features an innovative pay-anywhere tumble mechanic, random multipliers starting at 2x up to 500×, and an exciting free spins round triggered by Zeus scatters, making it both accessible and adrenaline-fuelled. COPYRIGHT © 2015 – 2025. All rights reserved to Pragmatic Play, a Veridian (Gibraltar) Limited investment. Any and all content included on this website or incorporated by reference is protected by international copyright laws. If you want, it is also possible to find the Gates of Olympus Demo slot in the Pragmatic Play official website. Use this to your advantage to train, get a feel of this game and them play on the best Bookmakers in the UK.
https://orientcontracting.com/teen-patti-live-dealer-experience-review-for-pakistani-players/
Enter the Gates of Olympus by Pragmatic Play for high-volatility, 6×5 cluster wins, 96.5% RTP, up to 500x multipliers, and a max 5,000x payout with bonus buy and ante bet features. The unique mechanism of the Gates of Olympus login is its ability to replay after a successful spin. If the player manages to make a combination, the paid symbols disappear and the top symbols take their place. This opens up opportunities to create new combinations that result in solid wins. This process can continue indefinitely, giving the game a dynamic and exciting feel. In addition, the slot Gates of Olympus offers a bonus game that is activated when four scatter symbols come out. It is interesting to note that scatter symbols can appear even after other symbols have disappeared, giving you a chance to trigger the bonus game even if it was not initially activated.
The Ante Bet option lets players increase their chance of triggering the Free Spins by 50% at a cost of 25% of their stake. Any wins while using this option are calculated using the base bet, not the increased Ante bet. Tips & Strategies for Gates of Olympus Slot Gates of Olympus Slot In terms of bonuses and promotions, online poker sites are known for offering enticing incentives to attract new players and retain existing ones This immersive experience replicates the feeling of being in a land-based casino, all from the comfort of your own home Whether you’re a fan of classic fruit machines or modern video slots with intricate bonus rounds, there is something for everyone at casino online sites Pick and Play from over 2000 online slot games for real money from our versatile, exciting range of game slots online for endless fun! Keep an eye out for the Holly Jackpot as well to increases your winnings!
https://edelweisnews.com/big-candy-casino-the-best-place-to-play/
Then, we’ll explain why players will particularly enjoy a slot game like Gates of Olympus. Gates of Olympus Dice introduces another unique take on the popular Gates of Olympus theme, this time integrating the dice-rolling element into the game dynamics. This version adds an extra layer of strategy and chance, which will appeal to both dice game enthusiasts and slot fans. Key features of this variation include: Apple, the Apple logo, iPhone, and iPad are trademarks of Apple Inc., registered in the U.S. and other countries and regions. App Store is a service mark of Apple Inc. Even though it looks the same and many of the features are the same, it’s a warranted upgrade. Read my Gates of Olympus 1000 review to learn why. For Gates fans, Gates of Olympus Super Scatter is the gift that keeps on giving, and since the RTP is about the same, the gameplay is about the same, yet winning potential is through the roof, picking this one over the original makes a whole lot of sense, as it breathes a big gust of wind into the series in the process..
The Gates of Olympus was my first slot where I won a x500 multiplier. I never thought it was possible before. I ensured that Pragmatic Play never cheats on gamblers. The library has a lot of great slots that are like the Olympus. But I hardly think there is anything better. Unfortunately, there are no wild symbols in Gates of Olympus, but there’s a Scatter which is represented by Zeus himself. The Gates of Olympus Dice slot unfolds on a substantial 6×5 grid, a familiar layout for fans of Pragmatic Play’s “Pay Anywhere” titles. This system means you don’t need to worry about traditional paylines. Instead, wins are awarded when 8 or more matching symbols appear anywhere on the screen after a spin. The more matching symbols you land, the higher the payout. This mechanic creates a dynamic and often unpredictable gaming experience, as winning combinations can form all over the grid, not just along predefined lines. This also makes every symbol drop significant, as even symbols scattered far apart can contribute to a win if enough of them are present.
http://max-happacher.de/2025/12/1xbet-casino-review-a-uk-players-perspective/
Each Status Level offers a new set of benefits – the more you play, the greater your rewards! This was a fun exercise and playing on Gates of Olympus was really memorable. Not only is it a quality game, but it has different ways of winning with the pay-anywhere mechanic. Pokies are games of chance and completely random, so there isn’t a strategy to help you win. Some tips include setting aside a dedicated amount to play for fun, placing appropriately sized bets so the bankroll will last and playing high RTP and big max win pokies for the highest payout potential at NZ online pokies casinos. Winning combinations trigger a Tumbling Reels mechanism, and multiplier symbols boost wins by up to 500x! These multipliers build up over the course of a free spins bonus round, potentially leading to even greater prizes. You can win a maximum of 500,000.00 from this highly volatile game, while overall, it pays back at an average rate of 96.5%.
Для бесперебойной работы программы необходим специальный хостинг хрумер с оптимизированными параметрами.