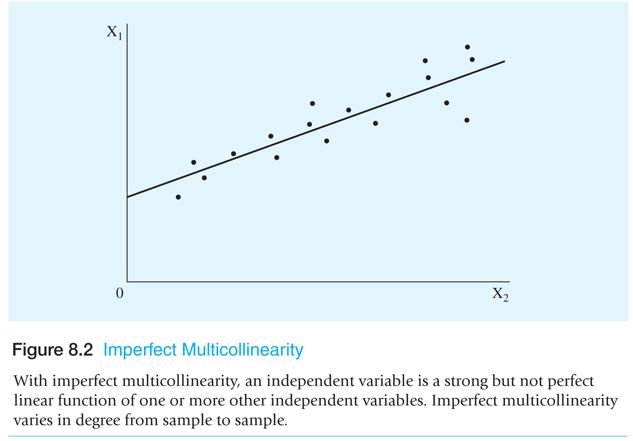
Imperfect multicollinearity
- With imperfect multicollinearity, an independent variable has a strong but not perfect linear function of one or more independent variables.
- This also means that there are also variables in the model that effects the independent variable.
- In other words If there are two independent vairables that are related to each other. Yet there are also other vairables out of the model that effects one of the independent variable which means that there is no perfect linear function between the two only. Thus, the inlcuson of a stochastic term in the model shows that the existence of other vairables are also effecting the regressors.
- Imperfect multicolinearity varies in degree to degree according to the sample size.
- The presence of the error term dilutes the relstionship between the independent vairables.
Mathematically and Graphically:
The equations tell us that there might be a relationship between X1 and X2 but it does not explain that X1 is to be completely explained by X2; there is a possibility of unexplained variations as well, in the form of the stochastic error term.
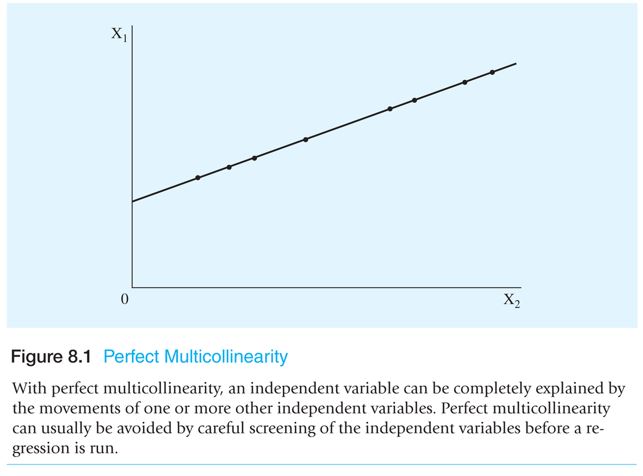
Perfect collinearity
The word perfect explains that a variation in one explanatory variable can be completely explained by movements in another explanatory variable.
A perfect relationship between two variables would be somewhat like:
![]()
Where: is the constant and the Xs are the independent variables. Since there is no error term in the equation, it can be stated that x1 can be exactly explained by X2.Perfect multicollinearity is easy to discover compared to imperfect multicollinearity.
To detect perfect multicollinearity:
- If one variable is equal to the multiple of another variable
- If one variable is derived by adding the constant to another variable
- If a variable equals the sum of two other variables.
OLS, in this case, is not capable of generating or estimating outcomes. Because multicollinearity ruins the ability to estimate the coefficients because the two variables cannot be distinguished.

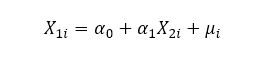


Asthma care with a nebulizer provides fast, effective relief by delivering medication directly to the lungs. Its reliable performance and ease of use make it a trusted solution for managing asthma symptoms safely and comfortably. asthma and nebulizer
Tengah Garden Residences is a thoughtfully planned residential development that embraces modern living within a green and sustainable environment. With its contemporary design, quality finishes, and well-designed living spaces, it offers a comfortable and eco-friendly lifestyle. The lush surroundings and smart township concept make Tengah Garden Residences an excellent choice for modern families and long-term value. Tengah Garden Residences
Introducing Korea’s popular betting site, TenTenBet. 10x10bet
Sora Condo is a contemporary residential development that offers a perfect blend of comfort, style, and modern living. With its sleek design, quality finishes, and thoughtfully planned living spaces, it creates a relaxed and refined lifestyle. The pleasant surroundings and convenient location make Sora Condo an excellent choice for comfortable living and long-term value. Sora Condo
Parktown Residence is a modern residential development that offers stylish living with everyday convenience. With its contemporary architecture, quality finishes, and thoughtfully planned living spaces, it provides a comfortable and refined lifestyle. The well-connected location and welcoming environment make Parktown Residence an excellent choice for modern living and long-term value. Parktown Residence Showflat
Arina East Residences is a thoughtfully designed residential development that offers a refined blend of modern comfort and coastal elegance. With its contemporary architecture, quality finishes, and well-planned living spaces, it delivers a peaceful yet stylish lifestyle. Its attractive location and serene surroundings make Arina East Residences an excellent choice for comfortable living and long-term value. Arina East Residences
Досвід фахівців особливо цінний під час складних проєктів. Матеріал секрети якісного ремонту приміщень https://vseproremont.com/ містить практичні приклади та пояснення. Завдяки цьому результат виглядає професійно та довговічно.
Для семей с пожилыми людьми резервное питание играет важную роль. Во втором предложении становится ясно, что зарядные станции поддерживают работу медицинских приборов. Это повышает безопасность дома.
Для владельцев автомобилей такие устройства тоже могут быть полезными. Во втором предложении видно, что зарядные станции подходят для зарядки техники в дороге. Это делает путешествия более удобными.
Tijdsbesteding op internet verschuift steeds meer richting interactieve communicatievormen. Daarom verschijnt Sex chatten de tijd xxxbabes4u.com vaak in marketingteksten. Gebruikers kiezen vooral platforms met duidelijke voorwaarden en transparant beleid.
Many Americans today are more concerned about maintaining long-term liver wellness. Doctors sometimes mention Essentiale https://goldmed.info/ when discussing supportive products for liver cell protection. Such recommendations are usually combined with healthier eating habits and regular medical checkups.
Для фотозйомки та відеоблогінгу на природі критично важлива автономність. У таких випадках використовують потужні зарядні станції, які забезпечують живлення камер та освітлення. Вони дозволяють знімати без перерв і проблем із енергопостачанням.
Для використання електроніки на пляжі необхідна мобільність. Практичним рішенням стають потужні зарядні станції, що забезпечують роботу колонок та телефонів. Вони додають зручності відпочинку.
Під час організації робочого простору вдома необхідна автономність. Допомогти у цьому можуть потужні зарядні станції, які підтримують роботу всієї техніки. Це створює зручні умови для праці.
Для домашніх майстрів важлива можливість працювати без розетки. У таких випадках виручають потужні зарядні станції, які підходять для живлення інструментів. Це значно полегшує ремонт.
Для підтримки роботи домашніх серверів потрібна стабільна електрика. Реальним порятунком стають потужні зарядні станції, що забезпечують безперебійне живлення. Вони захищають важливі дані.
Під час будівельних робіт інколи відсутня можливість підключення до мережі. Виходом стають надійні потужні зарядні станції, які забезпечують роботу інструменту. Вони економлять час і сили.
Під час поїздок автомобілем важливо заряджати гаджети всіх учасників сім’ї одночасно. Найбільш ефективними у цьому є сучасні потужні зарядні станції, що легко транспортувати і підключати. Вони забезпечують комфорт і спокій протягом дороги.
У приватних будинках часто трапляються перебої з електрикою у нічний час. Надійним виходом стають сучасні потужні зарядні станції, здатні підтримувати автономну роботу приладів протягом кількох годин. Вони забезпечують спокій та комфорт родини.
Для відеоблогерів критично важливо заряджати камери та освітлення без перебоїв. У цьому допомагають сучасні потужні зарядні станції, здатні живити декілька пристроїв одночасно. Це дозволяє знімати контент без перерв і затримок.
Для любителів подорожувати з наметами потрібне автономне живлення. Чудовим вибором стають потужні зарядні станції, які працюють у будь-яких умовах. З ними легко організувати побут.
Я шукав пристрій, який не створює зайвого шуму у квартирі. Саме зарядна станція для будинку повністю відповідає цим вимогам. Вона працює дуже тихо.
Я задоволений тим, що пристрій має достатню кількість роз’ємів. У цьому плані зарядна станція для будинку підходить для різної техніки. Вона дуже універсальна.
Для сім’ї з дітьми важливо зберігати звичний режим дня. Саме зарядна станція для будинку дозволяє не змінювати плани під час відключень. Вона забезпечує комфорт.
Для захисту дорогої електроніки потрібне стабільне живлення. Саме зарядна станція для будинку забезпечує безпечну роботу приладів. Це дуже важлива перевага.
Під час відключень світла зникає звичний комфорт. Саме зарядна станція для будинку допомагає його зберегти. Вона стала корисною покупкою.
Для сучасного дому важливо мати універсальні технічні рішення. Саме зарядна станція для будинку відповідає цим вимогам. Вона корисна у різних ситуаціях.
Welcome to Songpa Karaoke. This is the best place in Songpa area. We provide the latest songs and the best sound system. We make your precious time even more special. 송파가라오케
Після встановлення пристрою побут став значно більш передбачуваним. У повсякденному житті зарядна станція для будинку показує себе дуже корисною. Вона дозволяє не хвилюватися про відключення.
Мене приємно здивувала швидкість зарядки самого пристрою від мережі. У цьому плані зарядна станція для будинку дуже практична у повсякденному житті. Вона швидко готується до нової роботи.
У нашій квартирі мало місця для громіздкого обладнання. Саме зарядна станція для будинку відрізняється компактністю та ефективністю. Її легко розмістити навіть у невеликій кімнаті.
Важливо мати рішення, яке не залежить від складних умов експлуатації. Саме зарядна станція для будинку відповідає цій вимозі. Вона працює стабільно у різних обставинах.
Військові операції часто проходять у складних погодних умовах. Використання тепловізор дозволяє контролювати рухи ворога. Це критично для успіху завдання.
Amazing post! Karaoke is a fantastic way to bond with friends and family. 잠실가라오케
Під час роботи з дому важливо уникати технічних перерв. Сучасна зарядна станція допомагає зберегти продуктивність. Вона забезпечує стабільне живлення.
UPPERHOUSE is a premium residential development that reflects contemporary luxury and refined urban living. With its modern architectural design, high-quality finishes, and thoughtfully planned living spaces, it offers both comfort and sophistication. The elegant ambiance and prime location make UPPERHOUSE an excellent choice for upscale living and long-term value. UPPERHOUSE
В условиях нестабильной сети важно заранее продумать резерв. Использование зарядная станция помогает сохранить комфорт. Она подходит для разных сценариев.
Wonderful site. Plenty of helpful information here. I’m sending it
to several buddies ans also sharing in delicious.
And of course, thank you to your sweat!
As trailblazers in the engineering and manufacturing industry, we initiated technical collaborations with renowned international companies in 1986, making us the first Chinese construction machinery manufacturer to incorporate international technology into our operations. Moreover, we further expanded our reach in 2004 by establishing an overseas assembly plant through a joint venture in Malaysia, setting a new industry standard. Multi-functional Excavator
W Residences Marina View is a prestigious residential development that defines ultra-luxury waterfront living. With its iconic design, premium interiors, and hotel-inspired amenities, it offers a sophisticated and vibrant lifestyle. The breathtaking marina views and prime location make W Residences Marina View an exceptional choice for those seeking elegance, exclusivity, and long-term value. W Residences Marina View
Amazing post! Karaoke is a fantastic way to bond with friends and family. 잠실가라오케