Definition
“The standard deviation is defined as the positive square root of the mean of the squared deviations of the values from their mean.”
Characteristics of Standard Deviation:
i. The standard deviation is affected by the values of every observations.
ii. The process of squaring the deviations before adding, avoids the algebraic fallacy of disregarding signs.
iii. In general it is less affected by fluctuations of sampling than the other measures of dispersion.
iv. It has a specific mathematical meaning and could be easily adapted according to nature of algebraic treatment.
v. It has great practical utility in sampling and statistical inference.
Standard Deviation for Ungrouped Data
The standard deviation of a set of n values, ![]() denoted by S. The standard deviation for ungrouped data is mathematically represented as follows;
denoted by S. The standard deviation for ungrouped data is mathematically represented as follows;
For Example
Find the standard deviation for the values 2, 3, 6, 8 and 11.
Standard Deviation for Grouped Data
In case of a frequency distribution with ![]() as class marks and
as class marks and ![]() as the corresponding class frequencies, the standard deviation shall be calculated by using the following formula;
as the corresponding class frequencies, the standard deviation shall be calculated by using the following formula;
For Example
Find the frequency distribution for the frequency distribution of marks obtained by students provided in following Table 25
Table 25
|
Marks |
Frequency (f) |
Class Marks (X) |
fX |
|
20 – 24 |
1 |
22 |
22 |
|
25 – 29 |
4 |
27 |
108 |
|
30 – 34 |
8 |
32 |
256 |
|
35 – 39 |
11 |
37 |
407 |
|
40 – 44 |
15 |
42 |
630 |
|
45 – 49 |
9 |
47 |
423 |
|
50 – 54 |
2 |
52 |
104 |
For Example
Find the standard deviation of the weights distribution of 120 students in a University.
Short Method for Computing Standard Deviation:
From the above methods of calculating standard deviation, both grouped and ungrouped, we have noticed that computing standard deviation requires number of calculations which makes the task laborious. To make the difficult task easy, there is also a short method for computing standard deviation. Such short formulae are explained as follows;
Short Method for Ungrouped Data
The standard deviation for ungrouped data using short method, will be computed by using the following formula;
For Example
Find the standard deviation using short method for the values, 2, 3, 6, 8 and 11
n = 5
∑X = 2 + 3 + 6 + 8 + 11 = 30
Substituting the values in the formula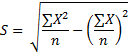
Short Method for Grouped Data:
The standard deviation for grouped data using short method, will be computed by using the following formula;
For Example
Find the standard deviation using short method for the values given in following Table 26
Table 26
| X | f | fX | ||
| 1 | 4 | 4 | 1 | 4 |
| 2 | 25 | 50 | 4 | 100 |
| 3 | 53 | 159 | 9 | 477 |
| 4 | 18 | 72 | 16 | 288 |
| 5 | 11 | 55 | 25 | 275 |
| 6 | 7 | 42 | 36 | 252 |
| 7 | 2 | 14 | 49 | 98 |

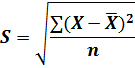
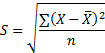
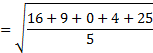
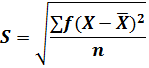
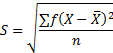
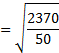
![clip_image042[1] clip_image042[1]](https://econtutorials.com/wp-content/uploads/2015/10/clip_image0421_thumb.png)
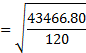
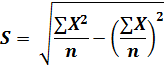
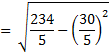
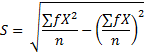
![clip_image070[1] clip_image070[1]](https://econtutorials.com/wp-content/uploads/2015/10/clip_image0701_thumb.png)
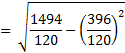


6085 872981Awesome inkling Grace! ego was luxurious youd bring about this about your biz bump into upstanding lineage. We reason you! 366300
245031 251416Obtaining the best Immigration Solicitor […]below youll locate the link to some internet sites that we feel you need to visit[…] 853631